• Démagnétiser l'aimant permanent
• Diamagnétisme

Densité de flux magnétique

La densité du flux magnétique représente, selon la définition spécifique, la densité des lignes de champ. Comme un soi-disant champ B, c'est une mesure indirecte de la force d'un champ magnétique. Pour mieux comprendre la définition, la désignation du champ B est nécessaire: ce n'est pas le vrai champ magnétique, même si les deux termes sont parfois utilisés de manière interchangeable dans la littérature.

Calculer la densité du flux magnétique

Alors que par définition la densité du flux magnétique est décrite par la lettre B, lettre du champ magnétique est H. Elle est appliquée avec les soi-disant constantes de perméabilité μ0 (par vide) etμ (pour des matériaux supplémentaires) on obtient le formule suivante:

La constante de perméabilité peut varier selon le type de matériau:

• Tant que le matériau n'est pas ferromagnétique, la constante de perméabilité spécifique du matériau μ est d'environ 1.
• Avec les matériaux ferromagnétiques cette valeur peut parfois atteindre 100 000.
• S'il s'agit à nouveau d'un supraconducteur, μ = 0 applique.

Le produit des deux constantes de perméabilité et du champ magnétique H détermine la définition de la densité du flux magnétique B. Elle est mesurée avec l'unité Tesla (T).

Informations de base

Beaucoup ne peuvent vraiment rien faire avec la formule de densité de flux magnétique mentionnée ci-dessus. L'explication descriptive du fond physique devrait aider un peu: un soi-disant champ magnétique se forme autour d'un conducteur à travers lequel l'électricité circule. Cela exercerait des forces sur le cobalt, le nickel, le fer ou d'autres matériaux ferromagnétiques à proximité. La densité du flux magnétique B indique à son tour la force de ce champ magnétique. Elle est aussi parfois appelée induction magnétique. B décrit la densité du flux magnétique à travers une surface. Il existe plusieurs formules pour effectuer ce calcul.

Densité de flux magnétique et flux magnétique - quelle est la différence entre les deux définitions?

La densité de flux magnétique qui traverse une surface imaginaire est le flux magnétique. Il est utile d'imaginer une image avec les lignes de champ magnétique entre deux pôles. La densité des lignes de champ dans une coupe transversale est quasi la densité de flux magnétique.

Selon les équations dites de Maxwell - une loi physique bien connue en électrodynamique - les lignes de champ ne peuvent pas simplement s'arrêter. La densité de flux d'un aimant continue donc de s'écouler. Le flux magnétique lui-même a le symbole de la formule Φ et indique essentiellement l'ensemble de toutes les lignes du champ magnétique. Le flux magnétique résulte donc d'une certaine zone A vers le produit de densité de flux magnétique B. La zone doit être perpendiculaire au flux.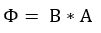

Les charges en mouvement - c'est-à-dire les courants - provoquent un flux magnétique. Cela n'a ni début ni fin, car les courants ne créent que des lignes de champ fermées. Physiquement correct, cela signifie qu'il n'y a pas de sources ou de puits dans le flux magnétique ou dans la densité du flux magnétique. C'est pourquoi deux pôles forment toujours un aimant: un pôle sud et un pôle nord.

Les équations de Maxwell en électrodynamique expriment ce fait mathématiquement. Il est important de comprendre que les aimants permanents s'appuient également sur ce comportement vis-à-vis de la densité de flux magnétique: c'est précisément ici que se forment des courants circulaires microscopiques avec un courant I, causée par les mouvements des électrons dans le matériau. Vous êtes responsable du flux magnétique ou du champ magnétique. Le courant circulaire crée un soi-disant moment magnétique avec le pôle sud en dessous de la boucle conductrice et le pôle nord au-dessus de cette boucle conductrice. Si la direction du courant était inversée, les pôles seraient inversés

D'un point de vue physique, le flux magnétique est donc défini par l'effet inductif qu'il exerce sur une boucle conductrice. Si une boucle conductrice avec une zone connue est amenée dans un champ magnétique, cela indique une surtension. Le flux magnétique est égal à l'intégrale de temps sur cette surtension: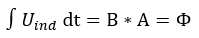

Le flux magnétique est mesuré avec cette boucle conductrice et la tension qui y est induite. Cependant, ce n'est plus une méthode courante: une sonde dite Hall est beaucoup plus précise. Si la densité de flux magnétique traverse une surface courbe, le flux magnétique doit être défini comme une intégrale sur la normale de surface de la densité de flux vectoriel:

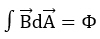Les lignes de champ qui entrent par une surface fermée - par exemple, la surface d'une sphère - doivent également en sortir. C'est la nature des lignes de champ fermées: r>Cela se manifeste mathématiquement par le fait que le flux magnétique à travers les surfaces fermées est toujours nul. Il n'y a donc pas de sources ou de puits dans la densité de flux magnétique.

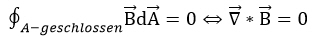L'équivalent de ceci est l'énoncé de l'une des quatre équations de Maxwell sur la soi-disant absence de divergence de la densité de flux magnétique.